Spiele, Simulation und dynamische Systeme

Analytische Methoden für nichtlineare und komplexe Systeme

Gegenüber der analytischen Behandlung von Systemen hat die Simulation einen entscheidenden Nachteil: Prägnante und aussagekräftige Merkmale von Schwingungen wie die Frequenz, der Dämpfungsfaktor und die sich schließlich einstellende Gleichgewichtslage müssen von Fall zu Fall ausgemessen werden. Die Ermittlung des Zusammenhangs zwischen den Werten der Systemparameter und diesen Merkmalen erfordert umfangreiche Messreihen und wird so zu einem mühsamen Unterfangen.

Simulation machen wir gerade dann, wenn die eleganten analytischen Methoden nicht mehr greifen: bei den sogenannten nichtlinearen Systemen. Das sind Systeme, in deren Systemgleichungen

die Zustandvariablen in den verschiedenen Termen der Funktion f nicht ausschließlich in der ersten Potenz vorkommen, sondern in denen beispielsweise Produkte von Zustandsvariablen und nichtlineare Funktionen derselben er-scheinen. Beispiel für ein lineares System ist die einfache Wachstumsgleichung . Nichtlinear hingegen ist die Gleichung für begrenztes Wachstum

Aber auch bei den nichtlinearen Systemen kommen wir - zumindest in Grenzfällen - mit analytischen Methoden weiter, wenn wir dem Systemverhalten gewisse Beschränkungen auferlegen. Das soll für das begrenzte Wachstum einmal durchexerziert werden.

Der Gleichgewichtspunkt

Der Gleichgewichtspunkt ist derjenige Zustand, in dem die Variablen des Systems konstant sind. Für unserer Wachstumsgleichung heißt das, dass die Wachstumsgeschwindigkeit null ist:

Das ist der Fall für N=0 oder für N=K. Der erste Fall ist uninteressant. Wir wollen den zweiten zugrunde legen.

Linearisierung im Gleichgewichtspunkt

Wir betrachten kleine Abweichungen vom Gleichgewichtspunkt und setzen N(t)=K+p(t) mit einer Funktion p(t), deren Werte wir beschränken - also klein halten - wollen, wenn sich dadurch Vereinfachungsmöglichkeiten ergeben. Der Ansatz wird in die Systemgleichung eingesetzt

(1)

Nach ein paar Vereinfachungsschritten und unter der Annahme, dass der Betrag von p(t) wesentlich kleiner als K ist, folgt daraus die näherungsweise gültige Systemgleichung eines linearen Systems:

(2)

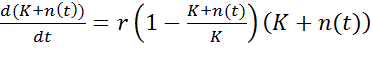
Diese Differentialgleichung mit dem Anfangswert lässt sich mit analytischen Mitteln lösen. Es ist

(3)

Übung: Vollziehen Sie den Übergang von (1) nach (2) nach (3) rechnerisch nach!

Die Anfangssteigung der Kurve (3) ist gleich (K-N(0))·r.

Übung:

(a) Erstellen Sie ein Arbeitsblatt Grenze.xls, in dem Sie die wirkliche Wachstumskurve N(t) sowie die Näherung K+p(t) simulieren, beide Kurven graphisch darstellen und die Tangente zu K+p(t) im Punkt t=0 einzeichnen. Freie Parameter: K, r, N(0) und Schrittweite h.

(b) Variieren Sie die Anfangswerte des Bestands und überprüfen Sie, inwieweit die eingezeichnete Gerade der Anfangssteigung der Kurve entspricht. Woran liegt es, dass die Gerade in manchen Fällen eine gute, und in anderen eine eher schlechte Annäherung an die Kurventangente ist? Geben Sie auch Anfangswerte vor, die oberhalb der Kapazität K liegen.

Zurück zur Gliederung