Spiele, Simulation und dynamische Systeme

Konkurrenz der Arten und Bedingungen für Koexistenz

Wechselwirkung zwischen zwei Populationen

Wenn zwei Populationen verschiedener Arten überhaupt Einfluss aufeinander haben, dann kann die Wirkung einer Art auf die andere positiv (+) oder negativ (–) sein; der neutralen Einfluss (0) bleibt hier einmal außer Betracht. Wenn beide Arten aufeinander negativen Einfluss haben (– –), spricht man von Konkurrenz, bei wechselseitig positivem Einfluss (++) von Kooperation oder Symbiose. Ist die Beziehung positiv für die eine und negativ für die andere Population (+–), dann haben wir es mit einer Räuber-Beute-Beziehung oder mit Parasitismus zu tun.

Die folgenden zwei Beispiele für Konkurrenzbeziehungen sind im Rahmen von Laborexperimenten genauer untersucht worden (Odum, 1991, 179 ff.).

Reismehlkäfer: Wenn man zwei Arten von Reismehlkäfern in einen Behälter mit Mehl setzt, stirbt eine Art früher oder später aus. Im selben Behälter können zwei Arten nicht überleben, auch wenn jede allein unter den gegebenen Bedingungen gut gedeiht. Die relative Anzahl der Individuen, die man zu Anfang in die Mischkultur einbringt, hat keinen Einfluss auf das Endergebnis. Unter heißen und feuchten Bedingungen setzt sich die eine Art durch, wohingegen die ander siegt, wenn es kühl und trocken ist. Wir haben es mit sog. Konkurrenzausschluß zu tun, bei der eine Koexistenz nicht möglich erscheint.

Kleesorten: Zwei in Schalen eng zusammengepflanzte Arten von Klee sind in der Lage, ihren Lebenszyklus vollständig zu durchlaufen und Samen zu produzieren, wenngleich die Dichte jeder Art geringer ist als in Reinkulturen. Kleine aber entscheidende Unterschiede in den Wachstumsformen ermöglichen die Koexistenz der Konkurrenten. Die eine Art wächst schneller und erreicht eher die maximale Blattdichte. Demgegenüber hat die andere Art längere Blattstiele und ihre Blätter sitzen weiter oben; so kann diese Art verhindern, im Schatten der anderen einzugehen.

Wir wollen Wachstumsgleichungen für zwei Populationen aufstellen, die in Konkurrenz miteinander stehen. Eine Simulation soll zeigen, ob sich das bei den Reismehlkäfern und bei den Kleesorten beobachtete Verhalten nachbilden lässt.

Die Konkurrenzgleichungen ergeben sich, wenn man in das Wachstumsgesetz für den Bestand N₁ der Population 1 die bestandsabhängige Zuwachsrate

(1)

einsetzt. Entsprechend erhält man das Wachstumsgesetz für den Bestand N₂ der Population 2, wenn man die bestandsabhängige Zuwachsrate

(2)

Ellipse: Ü wählt. Die Konstanten r₁ und r₂sind die Grundwachstumsraten der Populationen. Die Konstanten K₁ und K₂ sind Kapazitäten der Umwelt für die Populationen 1 und 2, jeweils unter der Bedingung, dass sie den Lebensraum allein besetzen.Der Parameter (die Konstante) a ist der Konkurrenzkoeffizient der Art 2 bezüglich der Art 1 und der Parameter ß ist der Konkurrenzkoeffizient der Art 1 bezüglich der Art 2.

Übung: Erstellen Sie ein Excel-Arbeitsblatt Konkurrenz.xls, um die Gleichungen für N₁ und N₂ zu simulieren.

Nun können wir mit dem Modell experimentieren. Wir haben insgesamt acht Parameter, die verändert werden können.

N₁	N₂	r₁	r₂	K₁	K₂	a	ß
Anfangswerte		Wachstumsraten		Kapazitäten		Konkurrenzkoeff.

Wie finden wir bei den vielen Variationsmöglichkeiten heraus, wann es zum Konkurrenzausschluss bzw. wann es zur Koexistenz kommt?

Ellipse: Ü Da wir die negative Methode anwenden wollen, beginnen wir grundsätzlich mit einer Vermutung, die wir dann mittels Experiment überprüfen.

Übung: Stellen Sie erste Vermutungen darüber auf, wann Konkurrenzausschluss und wann Koexistenz vorkommt und überprüfen Sie diese stichprobenartig am Excel-Arbeitsblatt Konkurrenz.xls. Notieren Sie insbesondere die zuerst plausibel anmutenden, dann aber falsifizierten Vermutungen, denn diese bringen Erkenntnisgewinn!

Gleichgewicht

Wir wollen zunächst herausfinden, inwieweit sich der beobachtete Konkurrenzausschluss mit dem Modell nachbilden lässt.

Vermutung 1: Der bei den Reismehlkäfern beobachtete Konkurrenzausschluss liegt daran, dass die Grundwachstumsraten r₁ und r₂ unterschiedlich sind. Wir setzen voraus, dass ansonsten jedes Individuum der eigenen Population die Wachstumsbedingungen in derselben Weise ändert, wie ein Individuum der anderen Population. Dem entsprechen die Konkurrenzkoeffizienten a = ß = 1. Auch die Kapazität ist für beide Populationen gleich.

Experiment: Wir führen die Simulation mit den Paramtern der folgenden Tabelle durch und stellen fest, dass die beiden Arten nebeneinander bestehen können. Es gibt nicht den vermuteten Konkurrenzausschluss, egal mit welchen Populationsgrößen man startet.

r₁	r₂	K₁	K₂	a	ß
0.1	0.11	500	500	1	1

Analyse: Eine Entscheidung zwischen den beiden Populationen ist im Bereich des r-Wachstums nicht zu erwarten: Beide Populationen wachsen, die eine halt etwas schneller als die andere. In der Nähe der Kapazitätsgrenzen müsste die Entscheidung kommen. Aber: Wenn eine der Populationen wächst, wächst auch die andere. Die Reduktion der Wachstumsraten in der Nähe der Kapazitätsgrenze reduziert die bestandsabhängigen Wachstumsraten beider Populationen gleichermaßen. Das beobachtete Verhalten des Modells erscheint nun plausibel. Wir verwerfen die Vermutung.

Vermutung 2: Eine Population verdrängt die andere, wenn sie den Lebensraum besser ausnutzen kann, also wenn für sie die Kapazität der Umwelt größer ist als für die Konkurrenten.

Experiment: Wir wählen die folgenden Parameter.

r₁	r₂	K₁	K₂	a	ß
0.1	0.1	500	450	1	1

In Bild 6 ist das Simulationsergebnis zu sehen. Wir stellen fest, dass es tatsächlich zum prognostizierten Konkurrenzausschluss kommt. Die Population 2 verschwindet selbst dann, wenn ihr Anfangsbestand viel größer als derjenige der Population 2 (wie im Bild zu sehen).

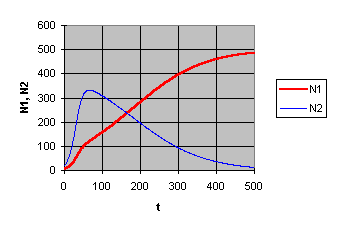
Bild 6 Konkurrenzausschluss durch unterschiedliche Kapazitäten

Analyse: Das im Modell beobachtete Verhalten entspricht dem im Labor an echten Lebewesen beobachteten. Das bestätigt unsere Vermutung und auch das gewählte Modell.

Vermutung 3: Die bei den Kleesorten beobachtete Koexistenz ist darauf zurückzuführen, dass die Wechselwirkung zwischen den Populationen vergleichsweise gering ist. Das heißt, dass die Konkurrenzkoeffizienten kleiner als Eins sind.

Experiment: Wir wählen die Parameterwerte der folgenden Tabelle. Im Experiment bestätigt sich die Vermutung: Unabhängig von den Anfangspopulationen stellt sich immer wieder derselbe Gleichgewichtswert ein, der für die Population 1 bei 385 und für die Population bei 231 liegt.

r₁	r₂	K₁	K₂	a	ß
0.1	0.1	500	500	0.5	0.7

Analyse: Die Vermutung ist bestätigt. Aber darüberhinaus haben uns die Experimente neugierig gemacht. Wir interessieren uns dafür, woher es kommt, dass sich bei unserem Modell immer wieder dieselben Endwerte einstellen, egal mit welchen Anfangswerten wir starten. Es muss sich um einen stabilen Gleichgewichtszustand handeln. Für die Untersuchung von Gleichgewichtszuständen eignet sich das sogenannte Zustandsdiagramm (hier N₁-N₂-Diagramm). Es ist in Bild 7 (linke Bildhälfte) zu sehen. (Das übliche t-N-Diagramm ist rechts daneben.)

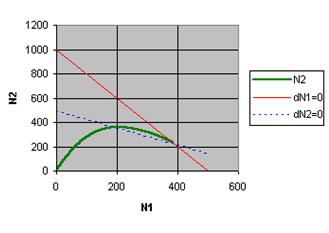
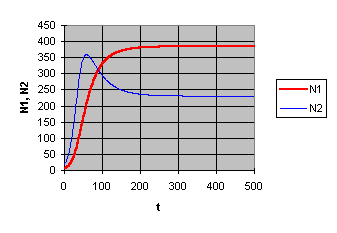
Bild 7 Koexistenz: ein stabiles Gleichgewicht. Links: Zustandsdiagramm, rechts: Zeitdiagramm.

Eingezeichnet sind die Nullwachstumskurven dN₁=0 für die Population 1 und dN₂=0für die Population 2. Sie sind durch die Gleichungen N₁ + a N₂ = K₁ (für dN₁=0) und N₂ + ß N₁ = K₂ (für dN₂=0) gegeben. Diese Gleichungen liefern Wertepaare (N₁, N₂), für die die jeweilige Population stagniert, also eine Wachstumsrate gleich null hat.

Im Schnittpunkt der beiden Kurven herrscht Gleichgewicht: beide Populationen stagnieren. Das Gleichgewicht heißt stabil, wenn bei allen Anfangswerten, die leicht vom Gleichgewicht abweichen, die Lösungen wieder zu diesem hinführen. Es heißt labil, wenn es in der Nähe liegende Anfangswerte gibt, bei denen die Lösung vom Gleichgewichtspunkt wegführt.

Es ergeben sich folgende Formeln für die Gleichgewichtswerte der Populationen:

Ellipse: Ü (3) N₁₀ = (K₁ - a K₂)/(1-a ß) und
(4) N₂₀ = (K₂ - ßK₁)/(1-a ß).

Übung: An welchen Punkten im N₁-N₂-Zustandsdiagramm herrscht Gleichgewicht? Leiten Sie einerseits die Gl. (3) und (4) her und finden Sie andererseits noch weitere Punkte, an denen Gleichgewicht herrscht. – HINWEIS: Gehen Sie zurück auf die (1) und (2) zugrundeliegenden DGLs.

Koexistenz

Die negative Methode fördert unser Verständnis der Theorie. Sie hat uns zuletzt auf ein für uns neues allgemeines Gesetz gebracht. Wir versuchen das Gesetz zu verallgemeinern. Wie sieht die Sache aus, wenn die Kapazitäten nicht mehr notwendigerweise gleich sind? Oder wenn ein Kopplungskoeffizient doch wieder größer als Eins wird? Wir stellen die folgende kühne Hypothese auf.

Vermutung 4: Immer wenn die Nullwachstumskurven sich im positiven Bereich (also für Populationsgrößen größer als null) schneiden, haben wir es mit einem stabilen Gleichgewicht zu tun. Im Gleichgewichtspunkt herrscht Koexistenz.

Experimente: Wir probieren mehrer Parameterkombinationen aus und stellen fest, dass die Vermutung sich oft bestätigt. Aber es gibt Gegenbeispiele. Zum Beispiel im folgenden Fall.

r₁	r₂	K₁	K₂	a	ß
0.1	0.1	500	500	1.5	1.5

Nur wenn beide Populationen mit exakt denselben Anfangswerten gestartet werden, läuft die Entwicklung auf den Gleichgewichtspunkt zu. Wenn die Anfangswerte voneinander leicht abweichen dann bleibt es im Bereich des r-Wachstums bei dieser leichten Abweichung.

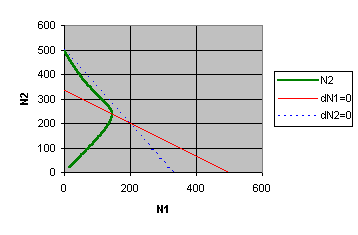
Bild 8 Konkurrenzausschluss: ein instabiles Gleichgewicht

In der Nähe des Schnittpunkts der Nullwachstumskurven kommt es zu einem radikalen Wechsel des Verhaltens: Die etwas größere Population geht innerhalb kurzer Zeit als Sieger aus der Konkurrenz hervor. Die andere wird vollkommen verdrängt. Hat die Population 2 einen leichten Startvorteil, dann setzt sie sich schließlich auch durch (labiles Gleichgewicht), Bild 8.

Analyse: Es kommt nicht nur darauf an, dass sich die Nullwachstumsgeraden im positiven Bereich schneiden. Die Vermutung ist also nicht präzise genug.

Wie lässt sich die Vermutung präzisieren? Vielleicht kommen wir mit einfachen Plausibilitätsbetrachtungen weiter. Eine Überlegung ist, dass sich Koexistenz einstellen könnte, wenn jede Population die andere weitgehend in Ruhe lässt, wenn also die Konkurrenzkoeffizienten verhältnismäßig klein sind. Wir präzisieren die Vermutung: Koexistenz ist genau dann möglich, wenn jedes weitere Individuum einer Population den eigenen Lebensraum um einen höheren Bruchteil reduziert als den der konkurrierenden Population.

Das lässt sich mathematisch fassen: Der Lebensraum (die Zuwachsrate) der Population 1 wird durch jedes weitere Individuum um den Bruchteil 1/K₁ reduziert. Jedes Mitglied der konkurrierenden Population 2 reduziert den Lebensraum der Population 1 um a /K₁. Für die Konkurrenzpopulation sind die entsprechenden Werte 1/K₂ bzw. ß/K₂. Die Bedingungen für Koexistenz lassen sich also folgendermaßen angeben: a /K₁ < 1/K2 und ß/K₂ < 1/K₁. Etwas umformuliert kommen wir zur

Vermutung 5: Die Bedingungen für Koexistenz sind K₂ < K₁/a und K₁ < K₂/ß.

Experimente: Wir führen mehrere Experimente durch. Alle bestätigen die aufgestellte Vermutung.

Ellipse: Ü Übung: Formulieren Sie die Bedingungen aus Vermutung 5 um, indem Sie das Verhältnis s = K₂/K₁ benutzen. Spielen also überhaupt die Kapazitäten eine Rolle dafür, ob Koexistenz möglich ist oder nicht? Was gilt für das Produkt aß ?

Analyse: Da es sich um eine allgemeine Aussage handelt, kann man noch nicht damit zufrieden sein, dass sie durch ein paar Experimente bestätigt wird. Wir suchen nach einer allgemeinen Begründung. Wir zeichnen die Nullwachstumsgeraden in ein N₁-N₂-Diagramm ein. Die in den Ungleichungen verglichenen Werte sind genau die Achsenabschnitte dieser Geraden, Bild 9.

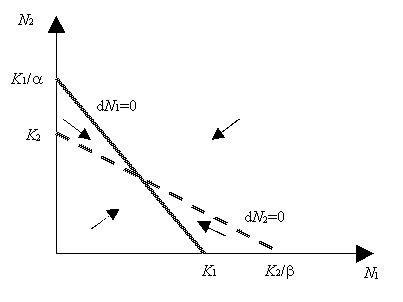
Bild 9 Veranschaulichung der Bedingung für stabiles Gleichgewicht

Das qualitative Systemverhalten lässt sich anhand der Nullwachstumskurven einfach bestimmen: Unterhalb dN₁ = 0 wächst die Population 1, oberhalb schrumpft sie. Dasselbe gilt für die Population 2 bezüglich der Nullwachstumsgeraden dN₂ = 0. Wenn die Nullwachstumsgeraden sich schneiden, gibt es im Zustandsraum vier Bereiche. Diese kann man durch die Wachstumsrichtungen der Populationen unterscheiden. Bild 9 zeigt den Fall, dass die oben aufgestellten Bedingungen für Koexistenz erfüllt sind. Man erkennt leicht, dass das Populationswachstum grundsätzlich in den Schnittpunkt der Geraden münden muss. (klar? – Z.B. gilt im dreieckigen Bereich oben links: dN₁>0 und dN₂<0. Deshalb müssen alle Richtungspfeile in Richtung Südost zeigen. Entsprechende Überlegungen gelten für die anderen Bereiche)

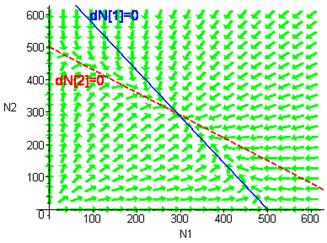
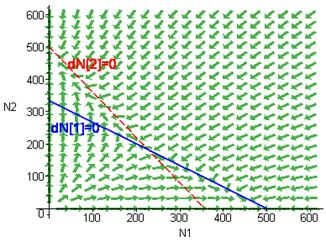
Einen noch besseren Überblick über das qualitative Lösungsverhalten erhält man, wenn man das Richtungsfeld der Differentialgleichungen darstellt (z.B. mit Maple erzeugbar). Wir zeigen die Richtungsfelder im Falle eines stabilen Gleichgewichts (a=ß =0.7, Bild 10a) und eines instabilen Gleichgewichts (a=ß =1.5 Bild 10b).

Wesentlich für stabiles Gleichgewicht ist also, dass in allen Bereichen die Richtungspfeile auf den Gleichgewichtspunkt zuweisen. Dies gilt nur, wenn die Linien sich so schneiden, wie in Bild 10a gezeigt (dN₁=0 über dN₂=0 links vom Gleichgewichtspunkt). In Bild 10b weisen die Richtungspfeile in den dreieckigen Bereichen vom Gleichgewichtspunkt weg, deshalb gibt es keinen stabilen Endzustand, sobald die Lösung einmal einen der dreickigen Bereiche "gestreift" hat.

Bild 10a stabiles Gleichgewicht Bild 10b instabiles Gleichgewicht

Maple-Source: myDfieldplot.mws.

Ellipse: Ü Übung:

1. Stellen Sie die Systemgleichungen für kleine Auslenkungen n₁(t) = N₁(t) – N₁₀ (und n₂(t) analog) aus dem Gleichgewichtszustand (N₁₀, N₂₀) auf, gemäß dem Rezept der Linearisierung! Hinweis: Beachten Sie folgende Identitäten:

(5) K₁ - N₁₀ - a N₂₀ = 0 und
(6) K₂ - N₂₀ - ß N₁₀ = 0

Ellipse: Ü 2. Fertigen Sie mit den gefundenen Systemgleichungen qualitative Plots des Richtungsfeldes im n₁-n₂-Zustandsdiagramm unter verschiedenen Annahmen für die Parameter. Was können Sie daraus lernen für die Bedingungen, unter denen Koexistenz möglich ist?

FAZIT

Mit dem "Werkzeugkasten"

· Zustandsdiagramm

· Nullwachstumskurven

· Richtungsfeld

haben wir eine Methodik kennengelernt, mit der wir allein graphisch eine Menge über das Verhalten von DGLs und damit dynamischen Systemen lernen können: Man zeichnet im Zustandsraum die Nullwachstumskurven, ihre Schnittpunkte bzw. geeignete Schnittpunkte mit den Koordinatenachsen sind Gleichgewichstpunkte. Über eine Analyse des Richtungsfeldes gewinnt man Aussagen über die Stabilität der Gleichgewichtspunkte

Anregungen für Diskussionen

1. Die Konkurrenz der Arten ist eine der wesentlichen Voraussetzungen jeglicher Evolution. Zur Auslese kommt es, wenn mehrere Arten miteinander um dieselben Ressourcen konkurrieren und wenn diese Ressourcen im Verhältnis zur Nachfrage knapp sind. Kurz: Selektion ist Folge der Konkurrenz um begrenzten Lebensraum.

2. Ein wesentliches Fazit zur Koexistenz ist: Koexistenz ist nur dann möglich, wenn die Wechselwirkungen der jeweils anderen Art auf die eigene nicht zu stark sind. Diskutieren Sie das im Kontext der Globalisierung (Wettbewerb von Produkten und Herstellern). Welche Maßnahmen sind geeignet, um die Wechselwirkungen zu dämpfen?

3. Konkurrenzausschluss und ökologische Nischen: Wenn sich zwei konkurrierende Arten in ihren Bedürfnissen zu ähnlich sind, wird eine von ihnen früher oder später vernichtet (Exklusion durch Konkurrenz). Sind die ökologischen Nischen (also die Ansprüche an Ernährung und andere Umweltfaktoren) der beiden Arten voneinander verschieden genug, dann können sie koexistieren.

4. Wie sehen die Bedingungen für Konkurrenzausschluss aus? Führen Sie Experimente zur Überprüfung der Annahme durch. Hinweis: Am besten geht man von einer logischen Negation der Bedingungen für Koexistenz aus.

5. Die Vereinfachungen unseres Modells: Beschränkung auf wenige aggregierte Größen und Effekte ("reduktionistische Sicht"), Vereinfachung der funktionalen Zusammenhänge, deterministische Betrachtungsweise. Welche Ergänzungen und Erweiterungen in methodischer Hinsicht wie in Bezug auf den Gegenstand der Betrachtung bieten sich an?

Zurück zur Gliederung