Spiele,
Simulation und dynamische Systeme
|
Das Räuber-Beute-System: Vernetzung
"Die
gesamte Gesellschaft opfert immer mehr Zeit für einen Verkehr, der es ihr
angeblich ermöglichen soll, Zeit zu sparen" (Ivan Illich, 1975).
"Schmeicheln
wir uns nicht so sehr mit unseren menschlichen Siegen über die Natur. Für jeden
solchen Sieg rächt sie sich an uns" (Friedrich Engels).
Einführung
Probleme:
Antibiotika machen Bakterien resistent. Direkte Nahrungsmittelhilfe ruiniert Volkswirtschaften
(Übervölkerung, kaputte Landwirtschaft). Großangelegte Bewässerungsvorhaben
führten zur Verbreitung der Bilharziose, der heute am weitesten verbreiteten
Tropenkrankheit (Blindheit, 200 Mio. Betroffene in der 3. Welt). Weitere
Beispiele: Die Politik der hohen Schornsteine; fehlende Fressfeinde (Kaninchen
in Australien; Waschbär in Deutschland). Unsere Umwelt ist ein vernetztes
System. Sie ist so kompliziert, dass wir die Konsequenzen unseres Tuns nie
vollkommen übersehen können. Gutgemeinte Taten können fürchterliche Rückschläge
zur Folge haben.
Ziel:
Nachhaltigkeit (Sustainability) bei der Nutzung der Ökosysteme.
Methode: Simulation
eines Räuber-Beute-Systems auf der Basis der Lotka-Volterra-Gleichungen
(Prototyp für ein vernetztes Ökosystem).
Das Räuber-Beute-System
N1 steht für den Bestand der
Räuberpopulation und N2 für den Bestand der
Beutepopulation. Angenommen sei, dass die Geburtenrate der Räuberpopulation
proportional zum Bestand der Beute ist. Mit der Proportionalitätskonstanten B1
für die Geburtenrate und mit der Konstanten D1
für die Sterberate der Räuberpopulation setzt man das Wachstumsgesetz der
Räuber in der Form
dN1/dt
= (B1 N2
- D1) N1
an. Das ist die erste der sogenannten Lotka-Volterra-Gleichungen. Mit der Geburtenrate B2 der Beutepopulation und der Proportionalitätskonstanten D2, die die Abhängigkeit der Sterberate der Beutepopulation von der Anzahl der Räuber vermittelt, nimmt das Wachstumsgesetz der Beutepopulation die Form der zweiten Lotka-Volterra-Gleichung an:
dN2/dt
= (B2 - D2N1) N2
Die Parameter der Lotka-Volterra-Gleichungen
werden folgendermaßen festgelegt:
B1 = 15×10-6/Jahr
D1 = 0,6/Jahr
B2 = 0,6/Jahr
D2 = 300×10-6/Jahr
Die Parameter des Modells sind so gewählt worden, dass
in etwa die Populationszyklen wiedergegeben werden, wie sie in dem
vieldiskutierten System auftreten, das vom Luchs und seiner Hauptbeute, dem
Schneehasen, gebildet wird (Wilson, Bossert, 1973).
Gleichgewichtswerte (dN1/dt
= dN2/dt = 0):
N1 = B2/D2 = 2 000
N2 = D1/B1 = 40 000
Verfeinerungen des Modells
Für die Beute führen wir eine Kapazitätsbeschränkung
ein
dN2/dt
= (B2 (K-N2)/K - D2N1) N2
Der Räuber wird bewirtschaftet
dN1/dt
= (B1N2 - D1) N1
- E
Hierin bezeichnet E die Ernte- bzw.
Jagdrate. Die Simulation zeigt, dass die Kapazitätsbeschränkung
(beispielsweise K = 100 000) das System stabilisiert: Es erreicht
von selbst seinen Gleichgewichtspunkt.
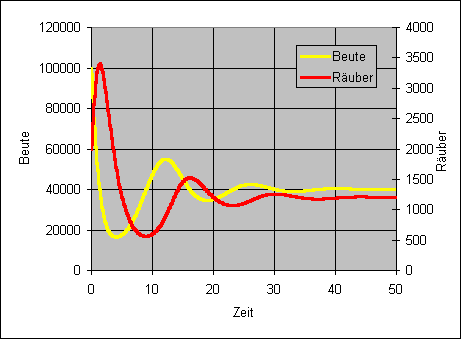
Das folgende Bild zeigt diesen Effekt im
Zustandsdiagramm. (Ein Zustandsdiagramm zeigt die Abhängigkeiten der
Zustandsvariablen - das sind hier die Populationsgrößen - voneinander.)
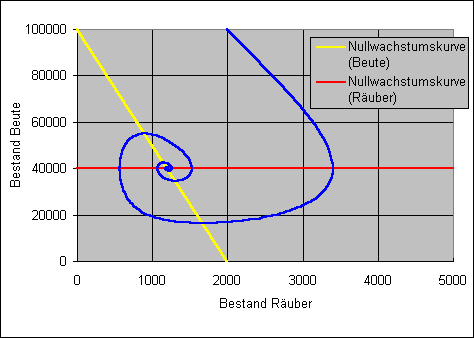
Wählt man das bestandsabhängige Jagen nach der
Strategie E = PN1, so bewirkt das nur eine
Erhöhung der Sterberate der Räuberpopulation um den Wert P. Das System
bleibt stabil. Man kann sich eine Ernterate P ausrechnen, bei der ein auf Dauer
erreichbarer Höchstertrag in der Ernte E erzielt wird (s. Übung 8), z.B. P=45%
für die hier gewählten Parameter.
Übungen, Analysen, Diskussionspunkte
1. Das
Räuber-Beute-System: Erstellen Sie ein Arbeitsblatt LotkaVolterra.xls zur Simulation des Räuber-Beute-Systems mit der Methode
der Zinseszinsrechnung. Führen Sie Berechnungsexperimente durch. Zur Überprüfung
des Ergebnisses: Im reinen Räuber-Beute-System ergeben sich periodische
Schwingungen für Räuber- und Beutepopulation.
2.
(anspruchsvoll): Die Simulation nach der Methode der Zinseszinsrechnung
(fachmännisch: "mit dem Verfahren nach Euler-Cauchy") muss zur
Erreichung der notwendigen Genauigkeit eine sehr kleine Schrittweite h
gewählt werden. Wenn dennoch mit der Simulation ein hinreichend großer
Zeitbereich erfasst werden soll (wenigstens eine Schwingungsperiode), wird die
Ablauftabelle sehr lang. Besser ist es hier, zu effizienteren Verfahren der
Integration der Differentialgleichungen (Lotka-Volterra-Gleichungen)
überzugehen. Geeignete Verfahren findet man in der Literatur zur numerischen
Mathematik. Nicht zu kompliziert und für die Tabellenkalkulation bestens geeignet
ist das Verfahren von Heun – ein Einschrittverfahren, das auf der Trapezregel
basiert (Stoer/Bulirsch, 1990).
3. Schädlingsbekämpfung:
Zeigen Sie mittels Simulation den Effekt, der folgendermaßen beschrieben wird: "Zum Beispiel ist Entomologen
aufgefallen, dass bei der Schädlingsbekämpfung durch Besprühen mit Insektiziden
die Population des Schädlings häufig zwar abnimmt, aber nur um dann sprunghaft
noch höher als zuvor anzusteigen. Dieses Phänomen ließ sich auf die
Mitvernichtung der natürlichen Räuber und Parasiten der Schädlingsart
zurückführen. Im Einklang mit dem Volterra-Prinzip sind diese nützlichen
Insekten nicht in der Lage, sich so schnell zu erholen wie die Populationen,
von denen sie leben" (Wilson/Bossert, 1973, S.
126 f.).
4. (a) Bestimmen Sie die
Gleichgewichtslage für das Räuber-Beute-System. (b) Zeichnen Sie die Nullwachstumskurven in die Zustandsdiagramme ein.
Nullwachstumskurven sind die geometrischen Orte im Zustandsdiagramm, für die dN1/dt=0
bzw. dN2/dt=0 ist. Wozu sind solche Kurven gut?
5. (a) Wie kann man aus den Zahlenkolonnen der Simulation heraus
die Länge eines Zyklus messen? (b)
(anspruchsvoller) Wie kann man die Länge des Zyklus andererseits analytisch
bestimmen? [Hinweis: Linearisieren des DGL-Systems für kleine Auslenkungen um
die Gleichgewichtslage, Beute-DGL einmal differenzieren und darin die
Räuber-DGL einsetzen.]
6. (a) Bei der Simulation ohne
Kapazitätsbeschränkung (oder bei K=¥, was
auf dasselbe hinausläuft) zeigen sich immer höhere Maxima bei Räuber- und
Beutepopulation. Das System "schaukelt sich also auf". Ist das
wirklich so, oder verhält sich die "wahre" Lösung der DGL anders und
das Aufschaukeln ist nur ein Artefakt numerischer Rundungsfehler?
(b) Können Sie Ihre Antwort aus (a) für
kleine Schwingungen um die Gleichgewichtslage herum auch analytisch begründen? [Hinweis:
Linearisierte DGLs aus Übung 5(b)
betrachten]
7. Stellen
Sie fest, für welchen Wert der Kapazitätsbeschränkung das Räuber-Beute-System
gerade aufhört zu schwingen (aperiodischer Grenzfall).
8.
(anspruchsvoll): Leiten Sie den aperiodischen Grenzfall für das linearisierte
System her.
9.
Diskutieren Sie die Literaturbeispiele über die Ökosysteme [Robbins04,
Beddington83] aus dem Blickwinkel der Lotka-Volterra-Gleichungen. Können Sie
den nachfolgend beschriebenen Effekt in der Simulation nachbilden: "Doch bis 1930 war die Population der
Wölfe ausgerottet – damals in voller Absicht, denn Wölfe galten als bedrohlich.
Durch die Wiedereinbürgerung dieses obersten Räubers in der Nahrungskette Mitte
der 1990er Jahre ... ist die Population der Wapiti [Rothirsche] inzwischen nur
halb so groß wie vor 15 Jahren." [Robbins04]
10. Zeigen
Sie, dass bei bestandsabhängigen Jagen des Räubers die höchste Ernte pro Jahr
bei einer Jagdrate von 45% erzielt wird (bei den oben gewählten Parametern).
Wie lautet die allgemeine Gleichung für die optimale Jagdrate?
|
|
Literaturhinweise
Robbins, J.: Wieder Wölfe im Yellowstone-Park.
Spektrum d. Wiss. (2004) 8, 24-29. Seit
im Yellowstone-Park wieder Wölfe leben, regeneriert sich das Ökosystem
verblüffend schnell. Auf die neue Situation reagierten unerwartet viele Tier-
und Pflanzenpopulationen – aber nicht alle gleich.
Beddington, J. R.; May, R. M.: Die Nutzung mariner
Ökosysteme. Spektrum d. Wiss. (1983) 1, 104-112. Der auf Dauer haltbare
Höchstertrag.
Bergerud, A. T.: Die Populationsdynamik von Räuber
und Beute. Spektr.
d. Wiss. (1984) 2, 48-54
Grams, T.:
Simulation. BI Mannheim 1992. Anhand des
Räuber-Beute-Systems werden einfache analytische Methoden der Modellvalidierung
demonstriert, beisielsweise die Linearisierung im Gleichgewichtspunkt (S.
75-79.
Illich, I.: Selbstbegrenzung. Rowohlt, Hamburg
1975
Peschel, M.;
Mende, W.: The Predator-Prey Model. Do We Live in a Volterra World? Akademie Verlag/Springer Verlag, Berlin 1986
Rolf, A.; Möller, A.: Sustainable Development:
Gestaltungsaufgabe für die Informatik. Informatik-Spektrum 19 (1996) 4, 206-213
Stoer, J.; Bulirsch, R.: Numerische Mathematik 2.
Springer-Verlag, Berlin, Heidelberg 1990. S. 113-118. Anfangswertprobleme,
Einschrittverfahren, lokaler Diskretisierungsfehler
Vester, F.: Ballungsgebiete in der Krise. DVA,
Stuttgart 1976
Wilson, E. O.; Bossert, W. H.: Einführung in die
Populationsbiologie. Springer, Berlin, Heidelberg 1973
|
|
© Timm Grams, 6.7.1999
©