Examples¶
this doc shows how to use SACOBRA_Py.
G06 with Inequality Constraints¶
This example can be found in sacobra_ineq.py:
import numpy as np
from gCOP import GCOP
from cobraInit import CobraInitializer
from cobraPhaseII import CobraPhaseII
from opt.sacOptions import SACoptions
from opt.idOptions import IDoptions
from opt.rbfOptions import RBFoptions
from opt.seqOptions import SEQoptions
from show_error_plot import show_error_plot
G06 = GCOP("G06")
cobra = CobraInitializer(G06.x0, G06.fn, G06.name, G06.lower, G06.upper, G06.is_equ, solu=G06.solu,
s_opts=SACoptions(verbose=1, feval=40, cobraSeed=42,
ID=IDoptions(initDesign="LHS", initDesPoints=6),
RBF=RBFoptions(degree=2),
SEQ=SEQoptions(conTol=1e-7)))
c2 = CobraPhaseII(cobra).start()
show_error_plot(cobra, G06, file="../demo/error_plot_G06.png")
fin_err = np.array(cobra.get_fbest() - G06.fbest)
print(f"final error: {fin_err}")
We first load G06 from the G-problem benchmark suite. G06 is a problem with 2 inequality constraints. The object CobraInitializer cobra is initialized with the G06 problem characteristica and its SACoptions are set:
40 function evaluations, seed 42, latin hypercube sampling (LHS) initial design with 6 points, cubic RBF with polynomial tail of degree 2, sequential optimization with constraint violation tolerance of \(10^{-7}\).
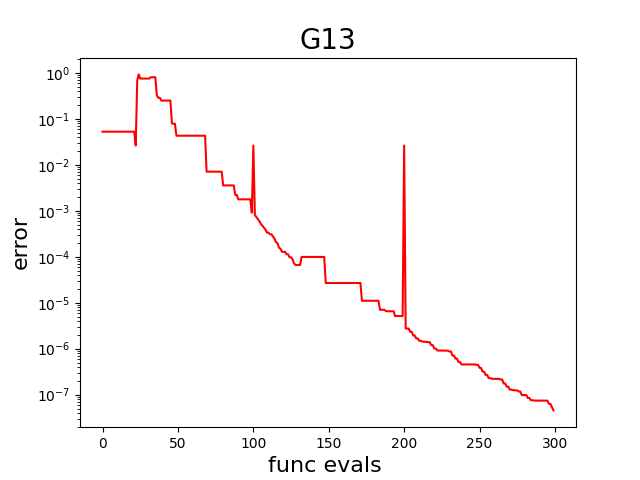
Now the optimization is started with CobraPhaseII. The object cobra is modified and enriched by this optimization: The data frames cobra.df and cobra.df2 are extended row-by-row with each iteration and they contain diagnostic information. The dictionary cobra.sac_res is extended as well: For example, the array cobra.sac_res['fbestArray'] has the evolution of the best fitness (objective) value over iterations. This is used by show_error_plot to display the error curve, which is also saved in PNG file error_plot_G06.png (click on image to enlarge):
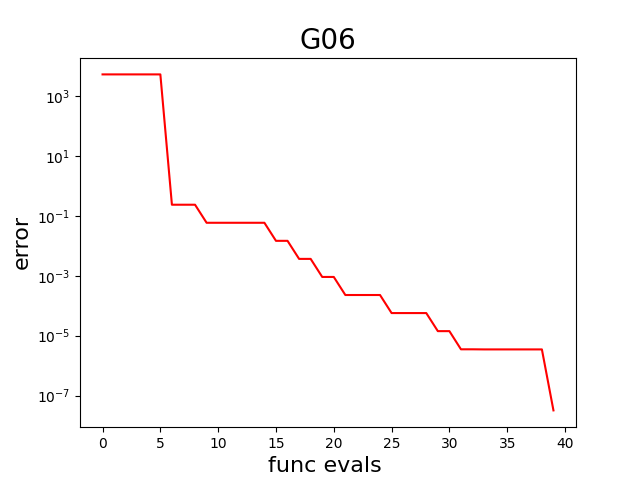
Finally, the final error (difference between the objective value found by the optimizer in the last iteration and the true objective G06.fbest) is computed and printed.
G13 with Equality Constraints¶
This example can be found in sacobra_equ.py:
import numpy as np
from gCOP import GCOP
from cobraInit import CobraInitializer
from cobraPhaseII import CobraPhaseII
from opt.equOptions import EQUoptions
from opt.sacOptions import SACoptions
from opt.idOptions import IDoptions
from opt.rbfOptions import RBFoptions
from opt.seqOptions import SEQoptions
from show_error_plot import show_error_plot
G13 = GCOP("G13")
cobra = CobraInitializer(G13.x0, G13.fn, G13.name, G13.lower, G13.upper, G13.is_equ, solu=G13.solu,
s_opts=SACoptions(verbose=1, feval=300, cobraSeed=42,
ID=IDoptions(initDesign="LHS", initDesPoints=6*7//2),
RBF=RBFoptions(degree=2, rho=2.5, rhoDec=2.0),
EQU=EQUoptions(muGrow=100, muDec=1.6, muFinal=1e-7,
refineAlgo="COBYLA"),
ISA=ISAoptions2(TGR=1000.0),
SEQ=SEQoptions(conTol=1e-7)))
c2 = CobraPhaseII(cobra).start()
show_error_plot(cobra, G13, file="../demo/error_plot_G13.png")
fin_err = np.array(cobra.get_fbest() - G13.fbest)
print(f"final error: {fin_err}")
We first load G13 from the G-problem benchmark suite. G13 is a problem with 3 equality constraints. The rest is very much the same as in the example before, except that the following new options in SACoptions are set:
RBFs start with smoothing factor \(\rho=2.5\) which means approximating RBFs. Parameter \(\rho=2.5\) is exponentially decaying towards 0 with factor
rhoDec=2.0. \(\rho=0\) or very small means interpolating RBFs.Equality handling with margin \(\mu\) (see
EQUoptions), where \(\mu\) is decaying exponentially with factor 1.6 from \(\mu_{init}\) towards \(\mu_{final} = 10^{-7}\), but re-growing everymuGrow=100iterations again to the large initial \(\mu_{init}.\) As refine algo (seeEQUoptions) we use “COBYLA” from packagenlopt.As an example we show how
ISAis initialized with derived classISAoptions2where all the defaults fromISAoptions2are taken, except that thresholdTGR=1000. (ISAoptionswould work as well, butISAoptions0would NOT work).
The resulting error curve in PNG file error_plot_G13.png looks like this (click on image to enlarge):