Probeklausur 2a - 2005
Aufgabe P.2.1(a)
| > | W:= (s,t) -> 180+5*s^2+10*t-0.2*s^3-0.3*t^2; |
![]()
Lokales Maximum bei s=100/6, t=100/6 der Höhe:
| > | W(100/6,100/6); |
![]()
Aufgabe P.2.1(b): Absolutes Maximum im Bereich bei
s=
![]() , t=100/6
der Höhe:
, t=100/6
der Höhe:
| > | W(-10,100/6); |
![]()
Aufgabe P2.2(a) Reihenfolge Gewichte: 0.1, 0.2, 0.25, 0.3, 0.55, 0.6, 1.0, 1.5, 1.7
Aufgabe P2.2(b) Reihenfolge Gewichte: 0.3 , 1.1 , 0.1 , 0.2 , 0.7 , 1.8 , 1.7 , 1.9 , 1.5
(Probe: Es müssen jeweils 9 Gewichte sein (wieso?) - Stimmt.)
Aufgabe P2.3(a)
| > | 1/22; |
![]()
Aufgabe P2.3(b). Die Standardabweichung
![]() ist (weil bis zum Punkt z=(180-150)/
ist (weil bis zum Punkt z=(180-150)/
![]() genau 70% der Normalverteilung aufgelaufen sein müssen, icdf = "inverse cumulated density function")
genau 70% der Normalverteilung aufgelaufen sein müssen, icdf = "inverse cumulated density function")
| > | with(stats): sigma:=30/statevalf[icdf,normald](0.7); |
Warning, these names have been redefined: anova, describe, fit, importdata, random, statevalf, statplots, transform
![]()
Probe: Ist
![]()
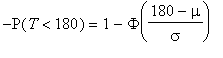 tatsächlich gleich 0.3?
tatsächlich gleich 0.3?
| > | 1-statevalf[cdf,normald]((180-150)/sigma); |
![]()
Stimmt!. (cdf = "cumulated density function", normald = "normal distribution")
Aufgabe P2.4(a)
| > | z1:=exp(1*I*Pi/3); z2:=exp(5*I*Pi/3); z3:=exp(9*I*Pi/3); |
![]()
![]()
![]()
Probe:
| > | simplify(z1^3); simplify(z2^3); z3^3; |
![]()
![]()
![]()
| > |
Aufgabe P2.4(b)
Aufgabe P2.4(b)
| > | restart: assume(n::integer); |
Damit Maple die Integrale vereinfachen kann, ist es wichtig, dass man die Bedingung n::integer einführt.
| > | t:='t': a:= n-> 1/Pi *(int(cos(n*t),t=-Pi..-Pi/3)+int(cos(n*t),t=Pi/3..Pi)); |
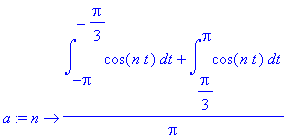
| > | simplify(a(0)); simplify(a(n)); |
![]()
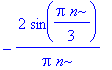
| > | t:='t': b:= n-> 1/Pi * (int(sin(n*t),t=-Pi..-Pi/3)+int(sin(n*t),t=Pi/3..Pi)); |
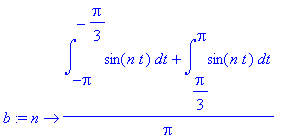
| > | simplify(b(n)); |
![]()
Mit welchem Argument erhält man das Resultat für b(n) ohne zu rechnen? - Weil f(x) gerade Funktion ist, aber alle Sinus-Funktionen ungerade.
Für die komplexen Fourierkoeffizienten gilt wg. b(n)=0:
c(0) = a(0)/2 und
c(n) = a(n)/2